As a kid, I was fascinated by geometric shapes, especially quadrilaterals. I remember spending hours drawing different kinds of squares, rectangles, and parallelograms. But it was the trapezoid and rhombus that truly captured my imagination. Their unique properties and the way they interacted with other shapes always felt like a puzzle waiting to be solved. In this article, we’ll delve into the world of these fascinating quadrilaterals, exploring their definitions, properties, and relationships.
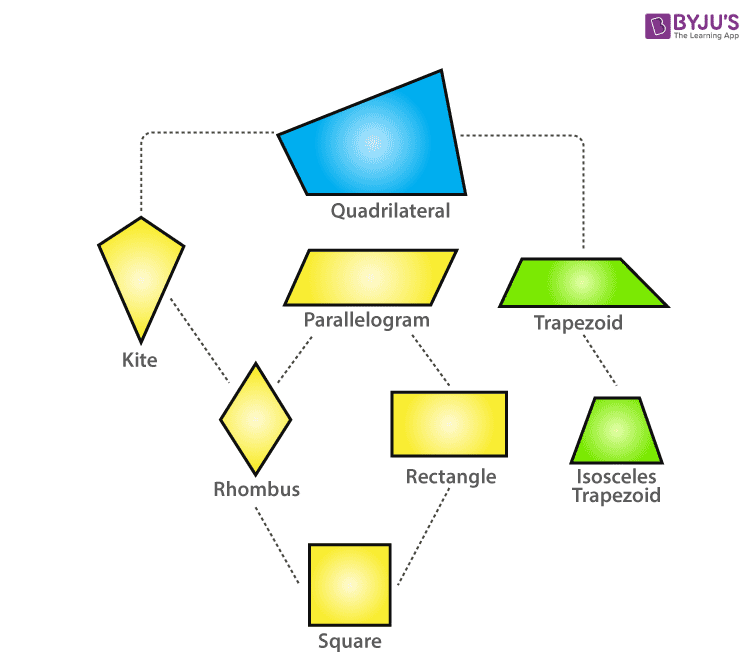
Image: byjus.com
You might encounter these shapes in everyday life, from the roof of a house to the tiles on your floor. Understanding their characteristics can help you appreciate the geometry that surrounds us and even use it to solve real-world problems.
Trapezoids: The Shapes with Parallel Sides
Defining a Trapezoid
A trapezoid is a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases of the trapezoid, while the other two sides are called legs. There are several types of trapezoids, categorized based on their angles and side lengths:
- Isosceles trapezoid: This trapezoid has congruent legs and congruent base angles. This means the angles at each end of each base are equal.
- Right trapezoid: This trapezoid has at least one right angle.
- Scalene trapezoid: This trapezoid has no congruent sides or angles.
The area of a trapezoid can be calculated using the formula: Area = (1/2) * (Base 1 + Base 2) * Height, where the height is the perpendicular distance between the two bases.
Rhombuses: Diamonds in Geometry
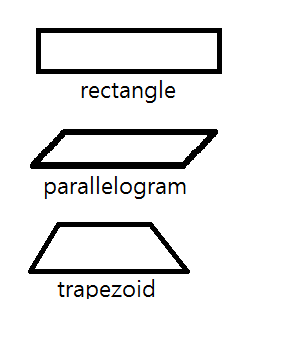
Image: microbiosrockbar.blogspot.com
The Properties of a Rhombus
A rhombus is a special type of quadrilateral where all four sides are congruent (equal in length). This means a rhombus is essentially a diamond shape. It possesses several unique properties:
- Opposite angles are equal: Like parallelograms, the opposite angles of a rhombus are congruent.
- Diagonals bisect each other at right angles: When you draw the diagonals of a rhombus, they intersect at a 90-degree angle and divide each other into two equal segments.
- Diagonals bisect the angles: Each diagonal of a rhombus bisects a pair of opposite angles, meaning it cuts the angle into two equal angles.
The area of a rhombus can be calculated using the formula: Area = (1/2) * (Diagonal 1 * Diagonal 2).
The Interplay of Trapezoids and Rhombuses
While distinct in their properties, trapezoids and rhombuses can share a connection. A special type of trapezoid called an **isosceles trapezoid** can create a rhombus when two of its vertices are joined to form a diagonal. This diagonal effectively divides the trapezoid into two congruent triangles and creates a rhombus using the base of the trapezoid and two sides of the triangles.
Real-World Applications of Trapezoids and Rhombus
These quadrilaterals are more than just academic concepts; they have practical applications in various fields:
- Architecture: Trapezoids are often found in building designs, from roof structures to window frames. Their stability and ability to distribute weight effectively make them ideal for architectural purposes.
- Engineering: Rhombuses are used in engineering to create stable structures like bridges and trusses. Their rigidity and ability to distribute force evenly are essential for these structures’ integrity.
- Art and Design: Both trapezoids and rhombuses are popular in art and design. Their distinctive shapes and symmetry can create visually appealing patterns and compositions.
Tips for Understanding Trapezoids and Rhombuses
Here are some tips to make learning about trapezoids and rhombuses easier:
- Visualize: Drawing diagrams and visualizing the shapes can help you understand their properties and relationships.
- Practice Problems: Solve practice problems to solidify your understanding and apply the concepts in different scenarios.
- Online Resources: Utilize online resources like interactive simulations and videos to explore these shapes in a dynamic and engaging way.
Remember, the key to understanding geometry is to be curious and proactive. Don’t hesitate to explore further, experiment with different shapes, and enjoy the beauty of mathematical patterns.
FAQ about Trapezoids and Rhombuses
Q: What are the differences between a trapezoid and a parallelogram?
A: A trapezoid has at least one pair of parallel sides, while a parallelogram has two pairs of parallel sides. A rhombus, which is a special type of parallelogram, has four equal sides, while a trapezoid does not.
Q: Can a rhombus be a trapezoid?
A: Yes, a rhombus is a special type of trapezoid where all four sides are equal. It has two pairs of parallel sides, meeting the criteria for a trapezoid.
Q: What is the difference between a rhombus and a square?
A: A rhombus has all sides equal, while a square has all sides equal and four right angles. All squares are rhombuses, but not all rhombuses are squares.
Trapezoid And Rhombus
Conclusion: Explore Further
Trapezoids and rhombuses are fascinating geometric shapes with unique properties and applications. By understanding their definitions, characteristics, and relationships, you can gain a deeper appreciation for the world around you. So, are you ready to further explore these intriguing quadrilaterals? Let your curiosity guide you as you delve further into the world of geometry!






