Have you ever found yourself staring at a pile of objects, trying to figure out how to divide them into equal groups? Perhaps you’re organizing a classroom for a project, arranging a backyard picnic, or even trying to understand the intricacies of a complex math problem. These scenarios all share a common thread – the need to find the greatest common factor (GCF). And while the concept may seem daunting, it’s actually a simple and incredibly useful tool that can make life a whole lot easier.
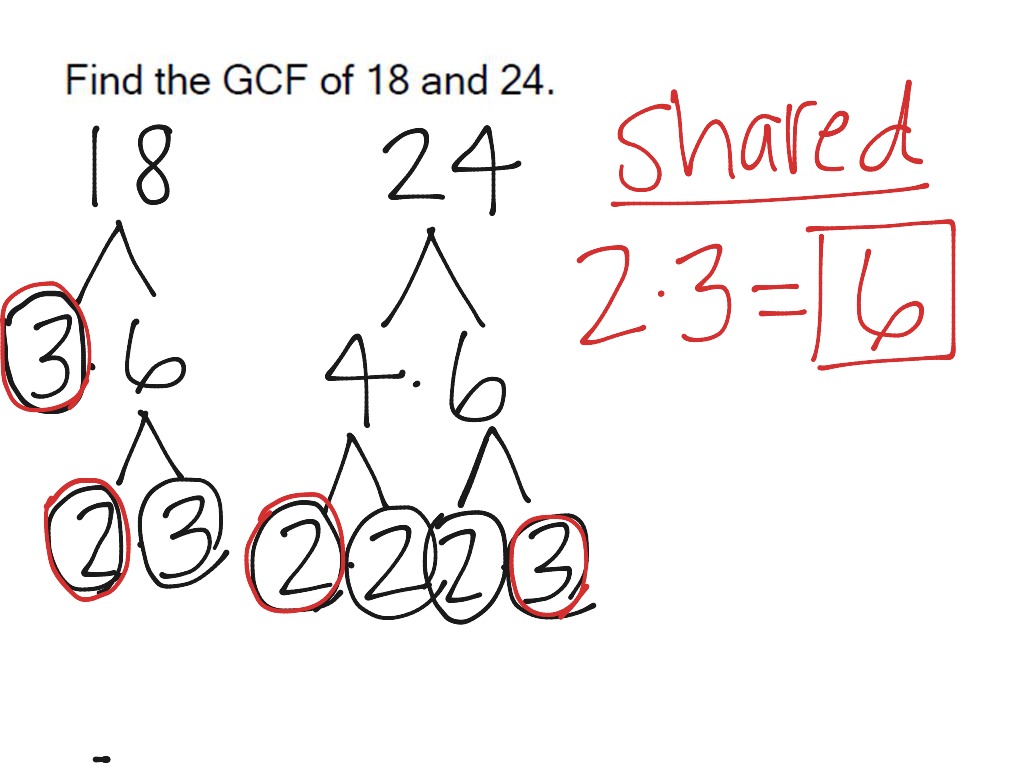
Image: www.showme.com
In this exploration, we’ll unravel the mystery behind finding the GCF of 24 and 40, shedding light on its relevance in everyday life and revealing the surprising power behind this seemingly simple mathematical concept. Whether you’re a student navigating the world of numbers or simply a curious mind eager to learn, this journey will equip you with the knowledge and confidence to tackle any GCF challenge that comes your way.
Understanding the Basics
The greatest common factor (GCF), sometimes called the highest common factor (HCF), is the largest number that divides into two or more numbers without leaving a remainder. It’s essentially the biggest factor shared by the numbers in question. To understand this more clearly, picture it like finding the largest piece of pizza you can cut from a bigger pie. The GCF is like that largest slice that fits perfectly into both pizzas.
Let’s take the example of 24 and 40. Their factors, which are the numbers that divide into them evenly, are:
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Notice that both numbers share the factors 1, 2, 4, and 8. But, the largest shared factor is 8, making 8 the GCF of 24 and 40.
Methods for Finding the GCF
There are a few tried-and-true methods to determine the greatest common factor, each with its own strengths and weaknesses. Let’s explore them:
1. Listing Factors:
This method, explained earlier, involves listing down all the factors of each number and then identifying the largest common factor. It’s a straightforward approach, especially for smaller numbers, but can become tedious when dealing with larger numbers.
2. Prime Factorization:
Prime factorization involves breaking a number down into its prime factors, which are prime numbers that multiply together to get the original number. Once we have the prime factorization of both numbers, we can simply multiply the common prime factors together to find the GCF.
For example, to find the GCF of 24 and 40 using prime factorization:
- 24 = 2 x 2 x 2 x 3
- 40 = 2 x 2 x 2 x 5
Both numbers share three factors of 2. Multiplying these together, we get 2 x 2 x 2 = 8, confirming our earlier finding that the GCF of 24 and 40 is 8.
3. Euclidean Algorithm:
The Euclidean Algorithm offers a more efficient method for finding the GCF, especially for larger numbers. It works by repeatedly dividing the larger number by the smaller number and noting the remainders. The GCF is then the last non-zero remainder. Let’s illustrate this with our example of 24 and 40:
- 40 divided by 24 leaves a remainder of 16.
- 24 divided by 16 leaves a remainder of 8.
- 16 divided by 8 leaves no remainder.
Therefore, the last non-zero remainder, 8, is the GCF of 24 and 40.
Beyond the Numbers: Applications of GCF
While finding the GCF might seem like a purely mathematical exercise, it has practical applications that permeate various aspects of our lives:
- Fraction Simplification: The GCF comes in handy when simplifying fractions. By dividing both the numerator and denominator by the GCF, we find an equivalent fraction in its simplest form. Consider the fraction 24/40, where the GCF is 8. Dividing both parts by 8, we get 3/5, which is the simplified form of the fraction.
- Sharing Equally: The GCF helps in dividing items into equal groups. For instance, if you have 24 cookies and 40 candies and want to divide them into equal groups, finding the GCF, which is 8, tells you that you can create 8 groups, each containing 3 cookies and 5 candies.
- Measurement Conversion: The GCF plays a role in converting between different units of measurement. For example, to convert from inches to feet, we need to know how many inches are in a foot (12). Finding the GCF of 12 and any number of inches helps us convert the measurement.
- Problem-Solving: GCF is a valuable tool for solving various real-world problems, such as finding the largest piece of fabric that can be cut from multiple rolls of different lengths, or determining the largest number of students that can be evenly distributed into groups for a school project.

Image: answer.ya.guru
Expert Insights and Actionable Tips
To further enhance your understanding and mastery of the GCF, let’s delve into some expert insights and actionable tips:
- Practice Makes Perfect: As with any mathematical concept, practice is key. The more you engage with GCF problems, the more comfortable you’ll become with the different methods and applications. Don’t shy away from challenging yourself with increasingly complex numbers.
- Visualization Aids: Visual aids like diagrams, charts, or even real-life objects can greatly simplify the understanding of GCF. Using manipulatives, such as blocks or counters, to divide into equal groups can make the concept more tangible.
- Connect with Experts: If you encounter difficulties, don’t hesitate to seek help from your teacher, tutor, or a math enthusiast. There are also numerous online resources and tutorials available for further support.
Gcf For 24 And 40
Conclusion
The greatest common factor is more than just a mathematical concept; it’s a fundamental tool that empowers us to navigate various everyday scenarios, from dividing items into equal groups to simplifying fractions and solving intricate problems. By understanding the different methods for finding the GCF, we equip ourselves with the knowledge and confidence to tackle any challenge that comes our way. So, the next time you find yourself facing a division problem or need to organize your belongings, remember the power of the GCF and unlock its hidden potential. And don’t be afraid to explore further; the world of numbers holds a treasure trove of knowledge just waiting to be discovered!






