Have you ever wondered how many times 8 fits into 56? It’s a simple question, but it unlocks a world of mathematical concepts and applications that shape our daily lives. From splitting a pizza with friends to calculating the cost of a bulk purchase, division plays a crucial role in our understanding and interaction with the world around us.

Image: materialcampusunfilial.z14.web.core.windows.net
This article delves into the fascinating world of 56 divided by 8. We will explore the basic principles of division, uncover its historical significance, and reveal how this seemingly simple calculation can be applied in real-world scenarios. We’ll also venture into the intricacies of advanced concepts, providing you with a comprehensive understanding of the magic that unfolds when 56 is divided by 8.
Understanding the Basics: The Essence of Division
At its core, division is the process of splitting a whole into equal parts. When we say 56 divided by 8, we are essentially asking: “How many groups of 8 can we make from 56?” This question can be visualized through various methods, such as:
- Drawing: Imagine you have 56 dots. Dividing them into groups of 8 would mean creating 7 sets of dots, each containing 8 dots.
- Real-Life Examples: If you have 56 candies and want to share them equally among 8 friends, each friend would receive 7 candies. 56 divided by 8 represents the number of candies per friend.
The History of Division: A Journey Through Time
Division has been a cornerstone of mathematics since ancient times. Babylonian mathematicians, as early as 2000 BC, employed complex methods to perform division. The Egyptians developed methods for dividing numbers using hieroglyphic symbols, while the Greeks further refined these techniques through their system of geometry.
The introduction of the Hindu-Arabic numeral system in the Middle Ages revolutionized division. The symbol “÷” was first used by the Swiss mathematician Johann Rahn in the 17th century. This symbol, alongside the concept of long division, greatly simplified the process of dividing large numbers.
The Power of Division: Real-World Applications
Division is a fundamental operation that finds applications in countless aspects of our lives. From everyday tasks to complex scientific calculations, division empowers us to make sense of the world around us. Some key applications of division include:
- Sharing: Whether splitting the cost of a meal with friends or dividing a cake among family members, division allows for fair and equal distribution.
- Measurement: Measuring a distance, calculating the time to travel a certain route, or determining the size of a garden plot all involve division.
- Finance: From calculating interest rates to determining the cost per unit of a product, division is essential for financial planning and transactions.
- Science and Engineering: Division plays a crucial role in scientific calculations, such as determining the average speed of an object or the density of a material.
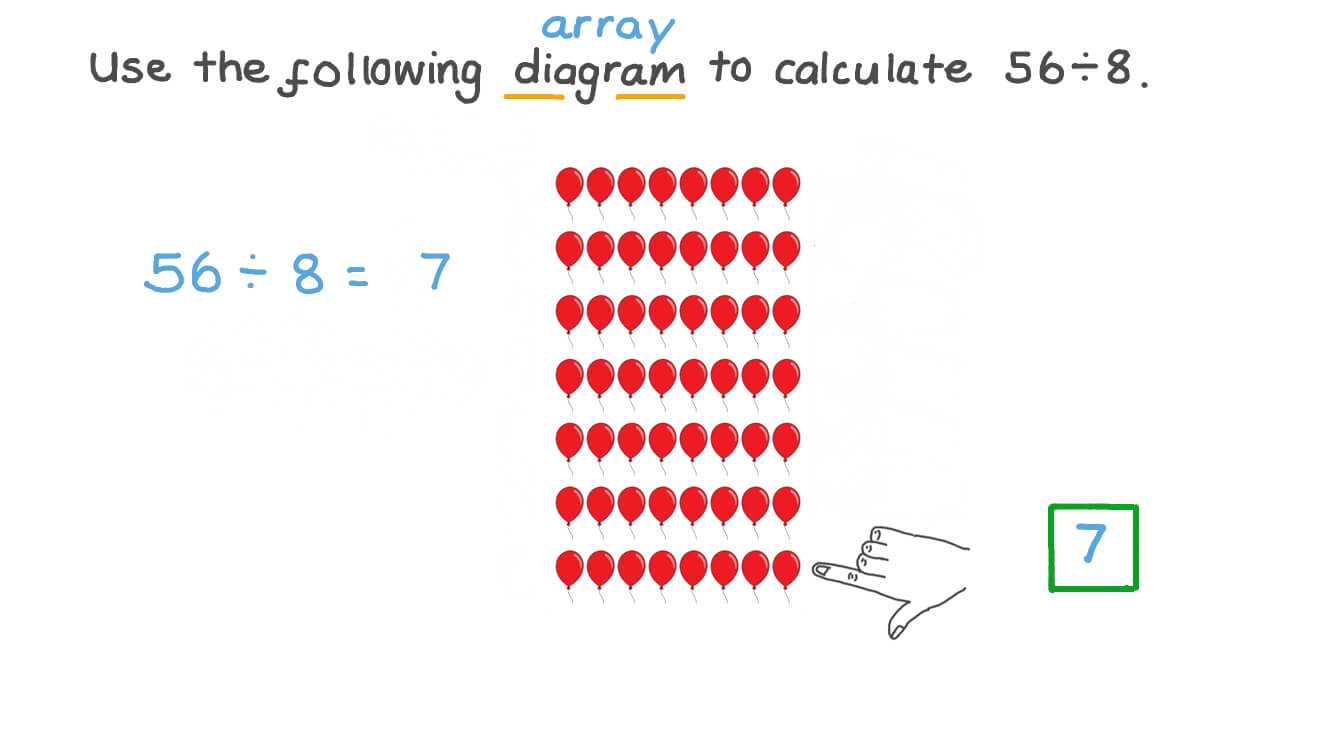
Image: www.nagwa.com
Beyond the Basics: Exploring Advanced Concepts
Beyond the basic understanding of division, there are numerous advanced concepts related to the topic. These concepts expand our understanding of division and its implications within the broader realm of mathematics.
1. Long Division
Long division is a systematic algorithm used to divide larger numbers. It involves a series of steps to repeatedly subtract the divisor from the dividend, keeping track of the quotient and remainder. This method is particularly useful for dividing numbers that are not easily divisible by mental calculation.
2. Fractions
Division can be represented as fractions. For example, 56 divided by 8 is equivalent to the fraction 56/8. This representation emphasizes the idea of representing a part of a whole. Understanding fractions allows us to work with numbers in a more flexible and versatile manner.
3. Decimals
Division can also result in decimals. If a number cannot be divided evenly into another number, the result will be a decimal. For instance, 56 divided by 5 yields 11.2. This decimal representation reflects the remaining part that cannot be divided into whole numbers.
56 Divided By 8
Conclusion
The seemingly simple act of dividing 56 by 8 unlocks a profound understanding of division, its historical significance, and its diverse applications. We have explored the fundamental principles, delved into historical advancements, and uncovered real-world scenarios where division plays a crucial role. From sharing resources to solving complex problems, division empowers us to make sense of the world and navigate our lives with greater clarity and efficiency. By embracing the power of division, we unlock a world of possibilities, allowing us to understand and shape the world around us.






