Have you ever been stuck trying to convert a fraction to a decimal? It can be a frustrating experience, especially when you need to work with numbers in different forms. Recently, I was helping my nephew with his math homework, and he struggled with converting 4/25 to a decimal. It made me realize that understanding how to do this can be a valuable skill, especially in everyday life. From calculating tips to measuring ingredients, decimals are everywhere! In this post, we’ll delve into the world of fractions and decimals, specifically explaining how to effortlessly convert 4/25 to a decimal. Let’s dive in!
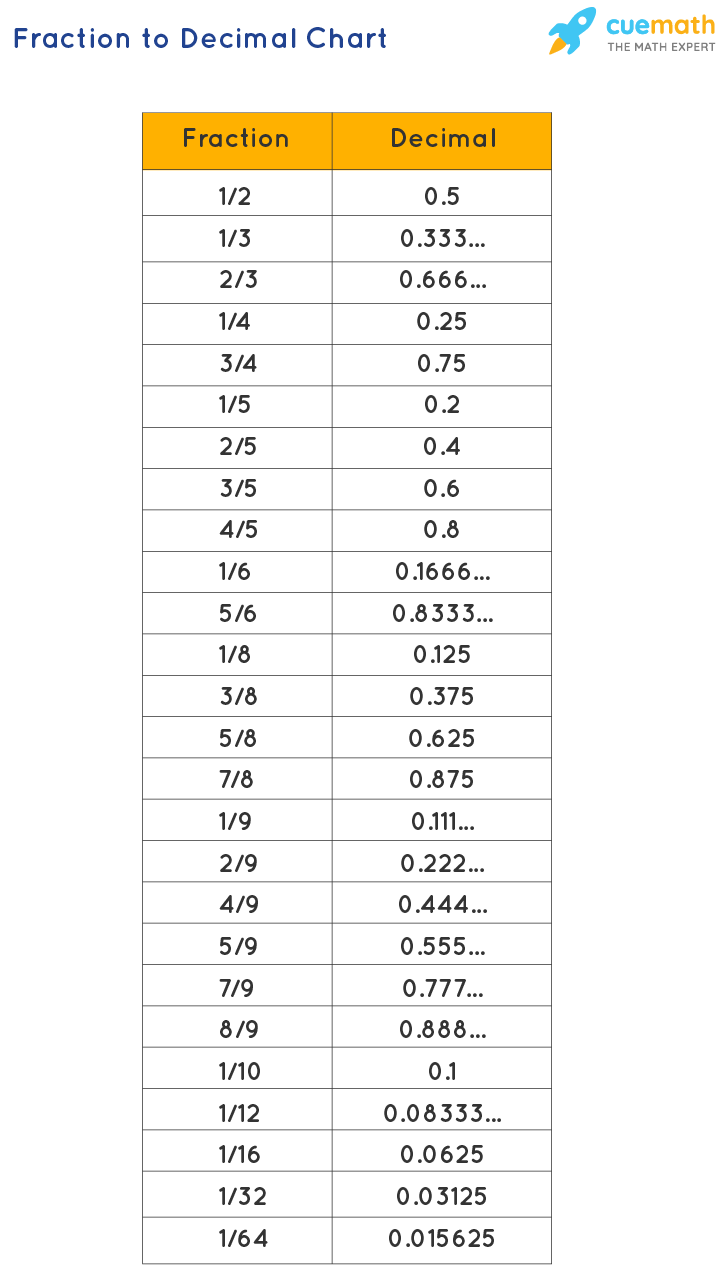
Image: www.aiophotoz.com
Understanding Fractions and Decimals
Before we tackle converting 4/25 to a decimal, let’s understand the basics of fractions and decimals.
A fraction represents a part of a whole number. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many parts we have, while the denominator tells us how many parts the whole is divided into.
A decimal is another way to represent a fraction. It uses a decimal point (.) to separate the whole number from the fractional part. Each digit after the decimal point corresponds to a power of ten, starting with tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
The Conversion Process: 4/25 as a Decimal
1. Dividing the Numerator by the Denominator
The key to converting a fraction to a decimal is to divide the numerator by the denominator. In the case of 4/25, we need to divide 4 by 25:
4 ÷ 25 = 0.16

Image: www.woodworkingtalk.com
2. Performing the Division
To perform the division, we can use long division or a calculator. We’ll demonstrate using long division:
- Set up the long division problem with 4 as the dividend and 25 as the divisor.
- Since 25 is larger than 4, we need to add a decimal point and a zero to the right of 4 (making it 4.0).
- Now, we can start the division process. We ask ourselves: how many times does 25 go into 40? We know that 25 goes into 40 once (1 x 25 = 25).
- We write 1 above the 0 in the quotient (the answer to the division problem) and subtract 25 from 40, which leaves us with 15.
- We bring down the next zero (0) from the dividend and now have 150.
- We ask ourselves: how many times does 25 go into 150? We know that 25 goes into 150 six times (6 x 25 = 150).
- We write 6 next to the 1 in the quotient and subtract 150 from 150, leaving us with 0.
- Since we have a remainder of 0, we stop the division process.
3. The Result
Therefore, 4/25 as a decimal is 0.16.
Important Tips for Converting Fractions to Decimals
- Remember the basics: Understanding the concepts of fractions and decimals is crucial for successful conversions. Review the definitions and their representations.
- Divide with confidence: Long division might seem daunting at first, but practice makes perfect! It’s a valuable skill to master for accurate conversions.
- Utilize a calculator: If you prefer a more straightforward approach, calculators can be handy for quick conversions.
- Look for patterns: If you’re working with fractions often, try to recognize common patterns that simplify the conversion process. For example, fractions with denominators that are powers of 10 (10, 100, 1000, etc.) are easily converted to decimals.
Expert Advice: Mastering the Skill of Converting Fractions to Decimals
Converting fractions to decimals is a fundamental math skill that can be applied in various situations. It’s not just about getting the right answer but also about understanding the relationship between different forms of numbers. Practice regularly, and consider exploring different methods to find the approach that suits you best.
Don’t be afraid to ask for help if needed. There are plenty of resources available online and in libraries that can provide further guidance and practice exercises.
FAQ: Common Questions About Fractions and Decimals
Q: Why is it important to know how to convert fractions to decimals?
A: Understanding how to convert fractions to decimals is crucial for various practical tasks, including:
- Calculation and Measurement: When working with measurements, such as in cooking or construction, converting fractions to decimals can make calculations more precise.
- Data Interpretation: Many charts and graphs use decimal representation, so understanding how to convert fractions enables easier interpretation and analysis of data.
- Financial Calculations: Financial transactions often involve decimals, particularly when dealing with interest rates, discounts, and currency exchange rates.
Q: What happens if the division doesn’t “end”?
A: If the division results in a repeating decimal (a decimal that goes on forever with a pattern), you can use a bar notation to indicate the repeating section. For example, 1/3 is 0.3333… and can be represented as 0.3.
4/25 As A Decimal
Conclusion
Converting fractions to decimals is a valuable skill that can simplify calculations, improve data analysis, and enhance your understanding of different number forms. Remember, practice makes perfect. With consistent practice and a clear understanding of the process, you can easily convert any fraction to a decimal, including 4/25, which is 0.16.
Are you ready to embrace the world of fractions and decimals with confidence? Let us know in the comments below if you have any further questions or if there are other fraction to decimal conversions you’d like to explore. We’re here to help you become a decimal conversion master!






