Have you ever encountered a sequence of numbers and wondered how to predict the next term? Imagine you are given the sequence: 2, 4, 8, 16… It’s easy to see that each term is twice the previous term. But what if the pattern is more complex? This is where the concept of recurrence relations comes in. Recurrence relations are powerful tools that define a sequence by expressing each term in terms of preceding terms. While understanding recurrence relations can be complex, a recurrence relation calculator can make the process more accessible and efficient.
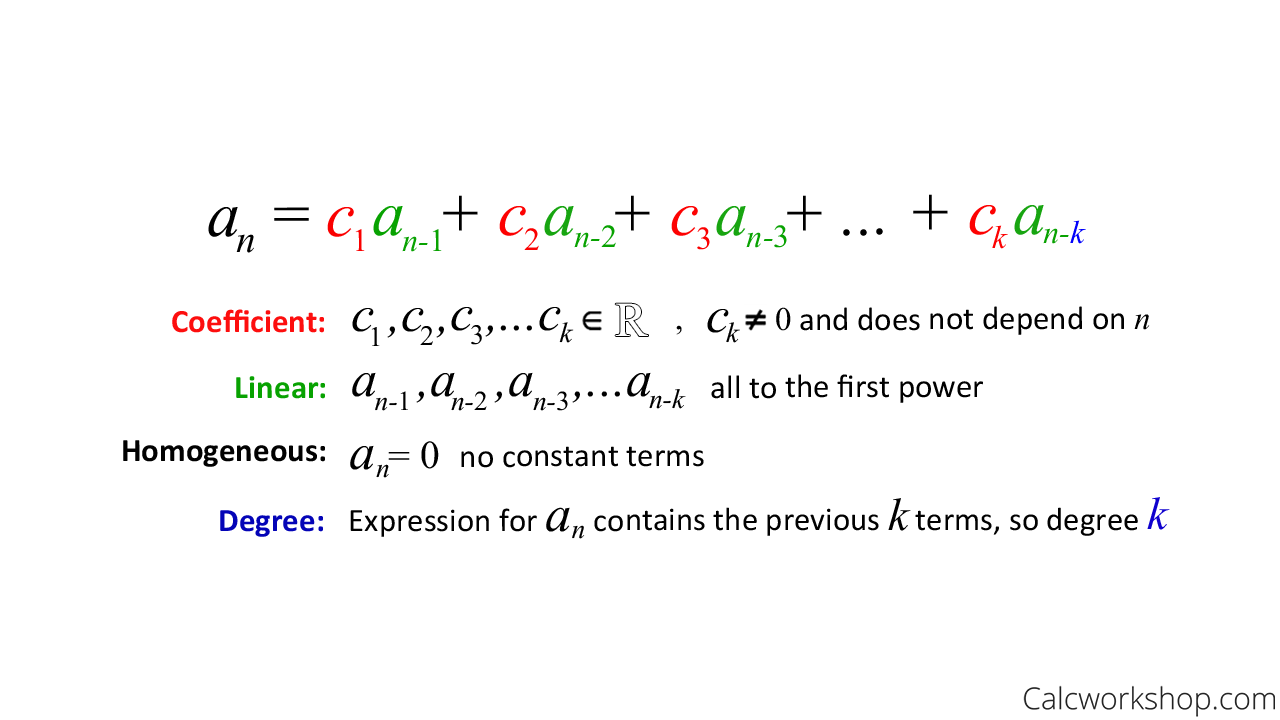
Image: ruebiemirab.blogspot.com
Fortunately, with the help of a recurrence relation calculator, you can easily find the explicit formula for a sequence and unravel the mysteries of its patterns, making it much easier to predict future terms. In this article, we’ll delve into the world of recurrence relations, exploring their significance, different types, and how to use a recurrence relation calculator to solve them.
Understanding Recurrence Relations
A recurrence relation is a mathematical equation that defines a sequence by expressing each term as a function of the preceding terms. This means that to find a specific term in the sequence, you need to know the values of the terms before it. Recurrence relations are widely used in various fields, including computer science, physics, and finance, to model and analyze phenomena involving sequential data.
Think of a recurrence relation like a recipe for creating a sequence, but instead of ingredients, you use previous terms to generate the next one. For example, the Fibonacci sequence is defined by the recurrence relation: F(n) = F(n-1) + F(n-2). This means that each term in the Fibonacci sequence is the sum of the two preceding terms.
Types of Recurrence Relations
Recurrence relations can be categorized based on their complexity and the way terms are defined. Here are some common types:
Linear Recurrence Relations:
- Homogeneous: All terms in the equation are multiplied by the sequence terms. For example: an = 2an-1 + 3an-2.
- Non-homogeneous: Contains a constant term that is independent of the sequence terms. For example: an = 2an-1 + 3an-2 + 5.

Image: www.slideserve.com
Non-linear Recurrence Relations:
- Involve powers of the sequence terms or other non-linear functions. For example: an = an-12 + an-2.
Recurrence Relation Calculator: Your Digital Assistant
Recurrence relation calculators are valuable tools for analyzing and solving sequences defined by recurrence relations. These online calculators typically require you to input the recurrence relation and any initial conditions. The calculator then uses mathematical algorithms to find the explicit formula for the sequence. Here’s how they work:
- Input the recurrence relation: Enter the equation representing the relationship between terms.
- Provide initial conditions: Specify the values of the first few terms in the sequence to set up the initial values.
- Calculate the explicit formula: The calculator will use a variety of techniques, such as generating functions, to find an explicit formula that expresses any term in the sequence directly in terms of the index (n).
- Generate terms: You can then use the explicit formula to calculate any specific term in the sequence.
Benefits of Using a Recurrence Relation Calculator
Using a recurrence relation calculator offers numerous advantages:
Saves Time and Effort:
Manual calculations for complex recurrence relations can be tedious and time-consuming. Calculators automate this process, saving you valuable time and effort.
Reduces Errors:
Human error is inevitable, especially when dealing with intricate mathematical calculations. Recurrence relation calculators minimize the risk of errors, ensuring accurate results.
Provides Insights:
By analyzing the explicit formula generated by the calculator, you can gain deeper insights into the behavior of the sequence, such as identifying patterns, growth rates, and limiting values.
Tips for Using Recurrence Relation Calculators
For optimal results when using a recurrence relation calculator, consider these tips:
- Choose the Right Calculator: Look for calculators specifically designed for recurrence relations, offering advanced features and accuracy.
- Understand the Input Format: Carefully read the instructions and use the correct syntax for inputting the recurrence relation and initial conditions.
- Interpret the Results: Pay close attention to the explicit formula generated by the calculator. Analyze the formula to gain insights into the sequence’s behavior.
- Validate Results: Manually calculate a few terms using the explicit formula to verify that the calculator has generated the correct answer.
FAQ
Q: What are some real-world examples of recurrence relations?
A: Recurrence relations are used in various fields:
- Computer science: They are used to analyze the efficiency of algorithms and data structures.
- Finance: They model the growth of investments and compound interest.
- Physics: They describe the movement of particles in a system.
Q: How do I choose the best recurrence relation calculator?
A: Look for calculators with the following features:
- User-friendly interface: Choose a calculator that is easy to use and understand.
- Advanced capabilities: The calculator should be able to handle complex recurrence relations.
- Accurate results: Ensure the calculator uses reliable algorithms to produce precise results.
Q: What are the limitations of recurrence relation calculators?
A: Recurrence relation calculators are helpful tools, but they have limitations:
- Limited scope: Calculators can only solve specific types of recurrence relations.
- Computational complexity: Solving complex recurrence relations can be computationally expensive.
Recurrence Relation Calculator
Conclusion
Recurrence relations are a fundamental concept in mathematics with broad applications across various fields. Understanding these relations can help us model and analyze sequential data effectively. Recurrence relation calculators are efficient tools that automate the process of solving recurrence relations, saving time and effort, while providing valuable insights into the sequence’s behavior.
Are you interested in learning more about recurrence relations? Let us know in the comments below!






