Remember those frustrating trigonometry problems in high school? I certainly do. One of the most challenging aspects, for me, was dealing with angles that weren’t standard values like 30°, 45°, or 60°. Calculating the values of trigonometric functions for those angles could be a real headache. Then, I discovered the magic of the half angle formula. This simple yet powerful formula allowed me to calculate the sine, cosine, and tangent of any angle, simply by knowing the values of their corresponding double angles. It was a game-changer, and it could be for you too.
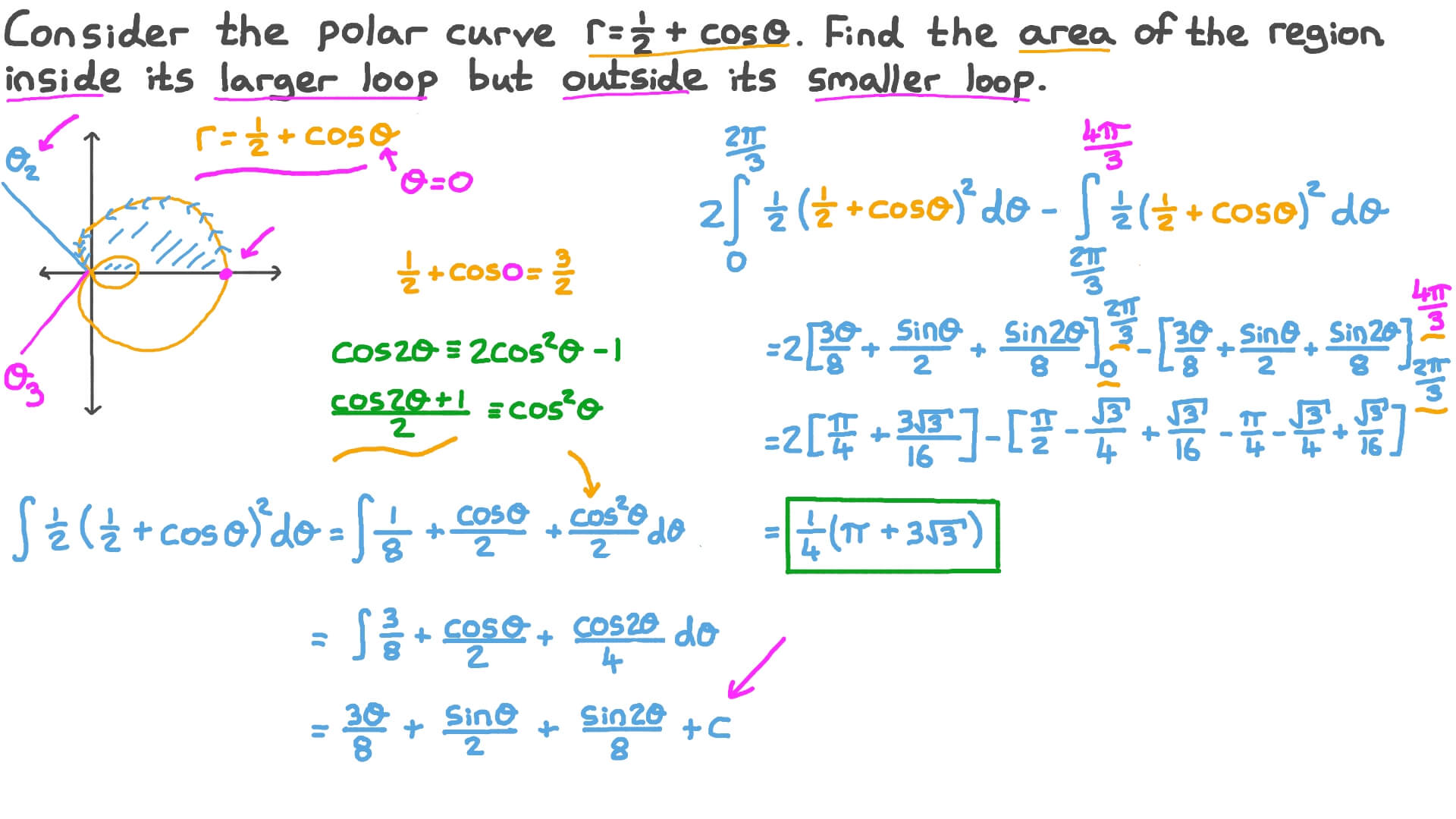
Image: mariemusammath.blogspot.com
Today, we’re going to dive deep into the world of the half angle formula and explore how it simplifies trigonometric calculations. We’ll discuss the formula itself, explore its applications, and even touch on the latest trends surrounding its use in various fields. Get ready to unlock the secrets of trigonometry with the help of your new best friend – the half angle formula calculator!
What is the Half Angle Formula?
The half angle formula is a set of three identities that express the sine, cosine, and tangent of half an angle in terms of the trigonometric ratios of the whole angle. The formulas are derived from the double angle formulas and are crucial in solving problems involving angles that are not standard values.
Here’s a quick breakdown of these formulas:
- Sine Half Angle Formula: sin(θ/2) = ±√((1-cosθ)/2)
- Cosine Half Angle Formula: cos(θ/2) = ±√((1+cosθ)/2)
- Tangent Half Angle Formula: tan(θ/2) = sin(θ)/(1+cos(θ))
The choice of sign (plus or minus) in the first two formulas depends on the quadrant of the angle θ/2. For instance, if θ/2 lies in the first quadrant, both sine and cosine are positive, and if it lies in the second quadrant, sine is positive and cosine is negative, and so on.
Understanding the Formula’s Mechanism
Derivation
The half angle formulas are directly derived from the double-angle formulas. Let’s understand the derivation of the cosine half-angle formula. Starting with the double angle formula for cosine, we know:
cos(2θ) = 1 – 2sin2(θ).
Replacing 2θ with θ, we get:
cos(θ) = 1 – 2sin2(θ/2).
Solving for sin2(θ/2), we get:
sin2(θ/2) = (1 – cos(θ))/2.
Taking the square root of both sides, we get the cosine half-angle formula:
sin(θ/2) = ±√((1 – cos(θ))/2).
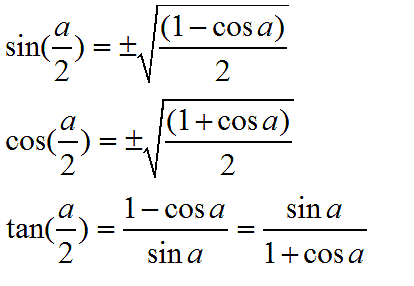
Image: ar.inspiredpencil.com
Applications
The Half Angle formula is a powerful tool that comes in handy in various scenarios. It’s particularly useful when:
- Calculating trigonometric values for non-standard angles: Imagine you need to find the sine of 22.5°. Since 22.5° is half of 45°, you can use the half-angle formula with θ = 45°.
- Simplifying complex trigonometric expressions: The half-angle formula can be used to simplify expressions involving trigonometric functions of angles that are not standard values. It helps to rewrite these expressions in terms of trigonometric functions of their double angles, which can be easier to deal with.
- Solving trigonometric equations: The half-angle formula can be used to solve equations that involve trigonometric functions of half angles. By substituting the half-angle formula into the equation, you can reduce the complexity of the equation and solve for the unknown variables.
- Calculus: The half-angle formula is also useful in calculus, particularly for solving integrals involving trigonometric functions.
Examples
Let’s look at an example of how to use the half-angle formula to calculate the sine of 15°:
We know that 15° is half of 30°. Applying the sine half-angle formula, we get:
sin(15°) = ±√((1-cos30°)/2).
Since 15° lies in the first quadrant, sine is positive. We also know that cos30° = √3/2. Substituting these values, we get:
sin(15°) = √((1-√3/2)/2) = √(2-√3)/2.
The Future of Half Angle Formula
The Half Angle Formula is a foundational concept in trigonometry. It has remained a critical tool for solving problems across different fields for centuries. As technology evolves and new applications emerge, the half-angle formula continues to be a crucial element in various areas.
Here are some key trends and potential developments concerning the Half Angle Formula:
- Artificial Intelligence and Machine Learning: AI systems are increasingly being used to solve complex problems, including those related to trigonometry. The half-angle formula can be integrated into AI models to improve their ability to handle trigonometric calculations and optimize solutions.
- Advanced Scientific Applications: Fields like physics, engineering, and astronomy heavily rely on trigonometry. The half-angle formula plays a vital role in these areas, enabling accurate calculations and analysis of data in various phenomena and applications.
- Education: The continuous development of educational tools, including online learning platforms and virtual reality applications, will likely see a greater emphasis on interactive learning experiences. This will lead to the creation of more engaging and accessible resources for understanding and applying the half-angle formula.
Tips and Tricks for Mastering the Half Angle Formula
I’ve spent a lot of time studying and working with the half-angle formula. Based on my experience, here are some tips and tricks to help you master it:
- Visualize the Unit Circle: A great way to understand the half-angle formula is to visualize it on the unit circle. Drawing the angles and their corresponding points helps you grasp the relationship between the half angle and the whole angle.
- Practice, Practice, Practice: The best way to become proficient with the half-angle formula is to practice solving problems using it. Start with simple examples and gradually increase the complexity.
- Use a Calculator: Don’t be afraid to use a calculator to help with calculations, especially for the square roots involved. This allows you to focus on understanding the concept rather than getting bogged down by calculations.
- Remember the Sign Convention: Pay close attention to the sign of the result based on the quadrant of the half angle. This is crucial to ensure you get the correct answer.
These tips can make your journey with the half angle formula more efficient and enjoyable. Remember, learning takes time and effort, so don’t get discouraged. With consistent practice and a bit of patience, you’ll be a master of the half angle formula in no time!
Commonly Asked Questions
Q: Can the half angle formula be used to find the values of any angle?
A: The half-angle formula can be used to find the values of any angle that can be expressed as half of another angle. If you can determine the trigonometric values of the double angle, you can use the half-angle formula to calculate the corresponding trigonometric values for the half angle.
Q: How do I know which sign to use in the half angle formula for sine and cosine?
A: The sign of the result for sine and cosine in the half-angle formula depends on the quadrant of the half angle. Remember the quadrants where sine and cosine are positive or negative, and choose accordingly.
Q: Is there an online calculator for the half-angle formula?
A: Yes, there are many online calculators available. These can easily calculate the values of trigonometric functions using the half-angle formula. Simply input the value of the whole angle, and the calculator will provide the values of sine, cosine, and tangent for the half angle.
Half Angle Formula Calculator
Conclusion
The half-angle formula is an indispensable tool for simplifying trigonometric calculations. It provides a systematic approach to dealing with angles that are not standard values. By understanding the formula and applying the tips we’ve discussed, you can unlock a whole new level of understanding in trigonometry. Are you ready to embrace the half angle formula and conquer those trigonometric challenges?
Are you interested in learning more about the half-angle formula, its applications, and its role in various fields? Let’s continue the conversation and explore the vast world of trigonometry together!






